[BOJ/1516] 게임 개발 - 풀이 및 코드

1516번: 게임 개발

문제

풀이 

 1번부터 N번 까지의 각 건물을 짓는데 드는 비용을 출력하면 되는 문제입니다. 단, 건물을 지을 때 특정 건물을 짓고 나서 건물을 지을 수 있는 경우가 있습니다. 즉, 건물을 짓는데 요구되는 요구사항 건물이 존재하는 것이죠.

 

 단순하게 생각하면, 최악의 경우 시간복잡도가 O(N^3)이 됩니다. A라는 건물을 짓기 위해서는 그 건물을 짓기 위한 요구 건물을 미리 지어야 하며, 여러 개의 건물을 동시에 지을 수 있기 때문에 A라는 건물을 짓기 위해서는 "요구되는 건물을 짓는 시간 중 가장 오래 걸리는 시간 + A건물을 짓는데 걸리는 시간"만큼의 시간이 걸립니다.
건물은 총 N개로, 최악의 경우, 1개의 건물을 짓는데 요구되는 건물이 N-1개 존재할 수 있으며, 그렇게 요구되는 N-1개 건물은 또, 각각 N-2, N-3, ..., 0개의 건물이 요구될 수 있습니다.  그런 건물이 N개가 존재하니 최악의 시간복잡도는 O(N^3)이 됩니다.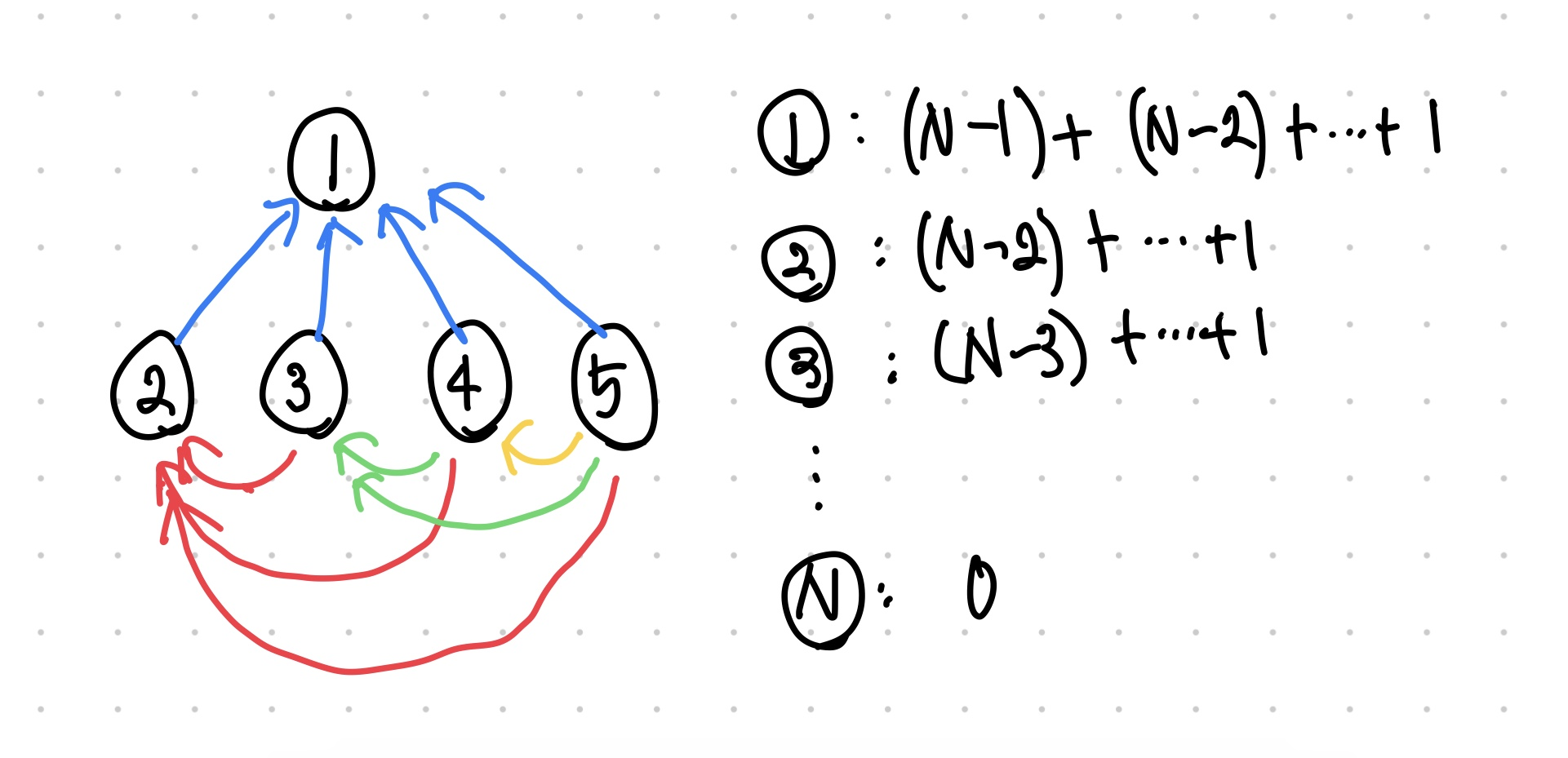

 

최악의 경우 시간복잡도 계산

 

 그래프 이론 중 사이클 개념이 존재하는데, 해당 문제에서는 건물들간의 관계에 사이클이 존재해서는 안됩니다. 사이클이 존재한다면 다음과 같은 상황이 연출됩니다.

 

 A라는 건물을 짓기 위해선 B라는 건물을 지어야 하고, B라는 건물을 짓기 위해선 C라는 건물을 지어야 하는데,  C라는 건물은 A라는 건물을 지어야 지을 수 있기 때문에 그 어떤 건물도 지을 수 없습니다. 원래라면 이런 사이클이 존재하는지 확인해야 하지만 해당 문제의 입력에서는 모든 건물을 반드시 지을 수 있다(사이클이 없음)는 조건이 있기 때문에 따로 생각하지 않아도 됩니다.

 

 그렇다면 어떻게 시간복잡도를 낮출 수 있을까요? 다이나믹 프로그래밍 기법으로 시간복잡도를 O(N^2)으로 낮출 수 있습니다. 

O(N^3)의 시간복잡도를 가지는 접근 방법 같은 경우엔, 건물의 건축 시간을 "기억하지 않고" 닥치는대로 모두 구했기 때문에 비효율적이였습니다. 만약 건물의 건축 시간을 구해놓고 그것을 기억한 다음, 이후에 또 그 건물의 건축 시간이 필요할 때 O(1) 내에 건축 시간을 구해 시간복잡도를 O(N^2)으로 줄일 수 있습니다.

 

 그렇게 접근하면, DP 테이블을 다음과 같이 정의할 수 있습니다.

만약, dp[v]가 정의되지 않았다면 재귀적으로 dp[v]를 구하면 됩니다. 이 부분은 코드를 보는게 더 직관적입니다!

코드 

코드 치팅은 BOJ 제재 사유입니다.

import sys
input = sys.stdin.readline

n = int(input().rstrip())
costs = [0 for _ in range(n+1)]
requirements = [[] for _ in range(n+1)]

for i in range(1, n+1):
    line = list(map(int, input().rstrip().split()))
    cost = line[0]
    costs[i] = cost
    # update requirements
    for j in range(1, len(line) - 1):
        requirements[i].append(line[j])

dp = [-1 for _ in range(n+1)]
# from root, get value of dp[v]. v is requirements of root node
# if dp[v] is not available, dfs that v node too.


def get_cost(root):
    requirements_cost = 0
    for v in requirements[root]:
        # if dp[v] is not available, dfs that v node too.
        # also save the return value of dfs at dp[v]
        if dp[v] == -1:
            dp[v] = get_cost(v)
        requirements_cost = max(requirements_cost, dp[v])
    return requirements_cost + costs[root]


# get_cost of every nodes
for i in range(1, n+1):
    if dp[i] == -1:
        dp[i] = get_cost(i)
    print(dp[i])